Alternative Tilings for the Fast Multipole Method on the Plane
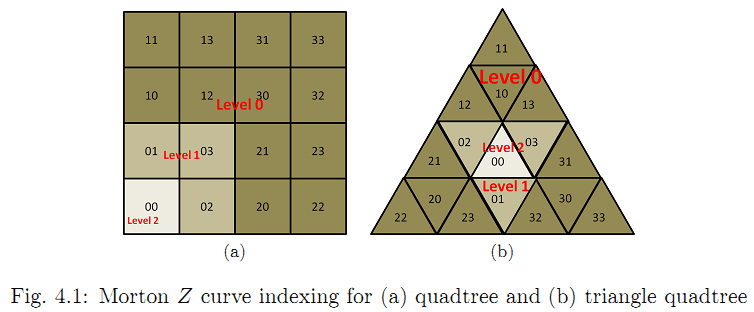
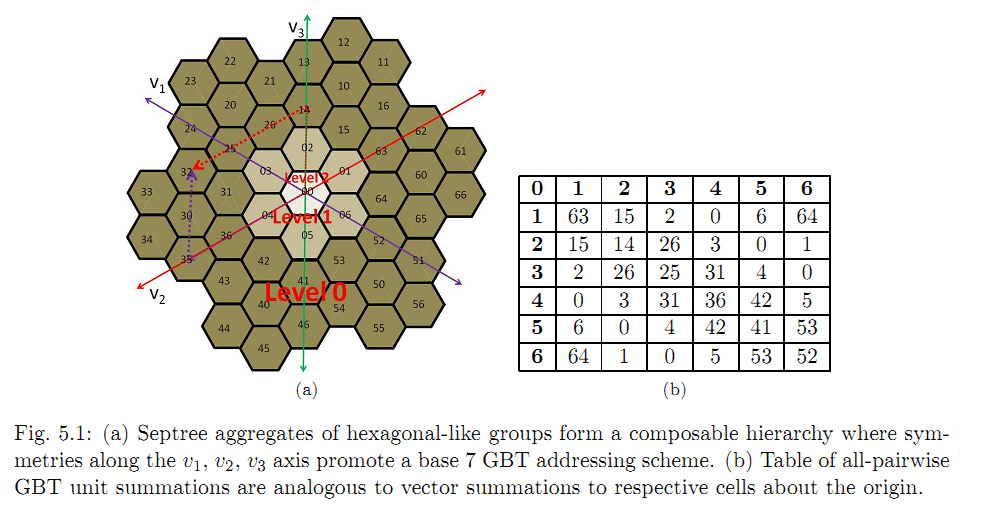
The fast multipole method (FMM) performs fast approximate kernel summation to a specified tolerance epsilon by using a hierarchical division of the domain, which groups source and receiver points into regions that satisfy local separation and the well-separated pair decomposition properties. While square tilings and quadtrees are commonly used in 2D, we investigate alternative tilings and associated spatial data structures: regular hexagons (septree) and triangles (triangle-quadtree). We show that both structures satisfy separation properties for the FMM and prove their theoretical error bounds and computational costs. Empirical runtime and error analysis of our implementations are provided.